Перевод из десятичной системы в любую другую

Перед тем как перейти к алгоритму перевода, вспомним алфавит популярных систем счисления:

Основание	Название	Алфавит
2	Двоичная	0, 1
8	Восьмеричная	0, 1, 2, 3, 4, 5, 6, 7
10	Десятичная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
16	Шестнадцатеричная	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Для перевода чисел из десятичной системы в любую другую, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.

Алгоритм перевода целых десятичных чисел в систему счисления с основанием q

1. Последовательно выполнять деление десятичного числа и получаемых целых частных на основание новой системы счисления, до тех пор, пока частное не станет равным 0.
2. Для получения ответа в q-ном коде, необходимо записать, полученные, в результате деления остатки, в обратном порядке.

Пример 1: перевести десятичное число 101 в двоичную систему счисления

Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:

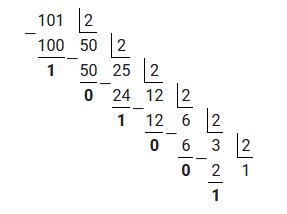
Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.

Ответ: 101₁₀=1100101₂

Пример 2: перевести десятичное число 443 в пятеричную систему счисления

Аналогично предыдущему примеру, произведем деление «столбиком». Решение будет выглядеть следующим образом:

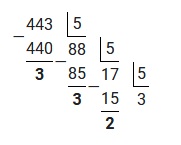
Полученные остатки необходимо записать в обратном порядке.

Ответ: 443₁₀=3233₅

Пример 3: перевести десятичное число 1187 в девятеричную систему счисления

Решение будет выглядеть следующим образом:

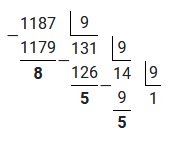
Ответ: 1187₁₀=1558₉

Алгоритм перевода десятичной дроби в q-ичную систему

1. Последовательно выполнять умножение исходной дроби на q, до тех пор, пока, дробная часть не станет равна 0 или пока не будет достигнута необходимая точность вычисления.
2. Полученная дробь в q-ичной системе будет равна прямой последовательности целых частей произведений.

Пример 4: перевести число 0,15 в троичную систему.

Решение будет выглядеть следующим образом:

0.15 ∙ 3 = 0.45 (0)
0.45 ∙ 3 = 1.35 (1)
0.35 ∙ 3 = 1.05 (1)
0.05 ∙ 3 = 0.15 (0)
0.15 ∙ 3 = 0.45 (0)
0.45 ∙ 3 = 1.35 (1)
0.35 ∙ 3 = 1.05 (1)
0.05 ∙ 3 = 0.15 (0)
0.15 ∙ 3 = 0.45 (0)
0.45 ∙ 3 = 1.35 (1)
0.35 ∙ 3 = 1.05 (1)

В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.

Ответ: 0.15₁₀=0.01100110011₃

Перевод дробного десятичного числа в q-ичную систему

Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.

Пример 5: перевести число 358,201 из десятичной системы в шестиричную

Для решения примера потребуется отдельно перевести 358 и отдельно 0,201 из десятичной системы в шестиричную, используя вышеизложенные алгоритмы. Таким образом переведя 358, получим:

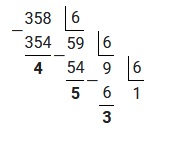
358₁₀=1354₆

Перевод десятичной дроби 0,201 выглядит так:

0.201 ∙ 6 = 1.206 (1)
0.206 ∙ 6 = 1.236 (1)
0.236 ∙ 6 = 1.416 (1)
0.416 ∙ 6 = 2.496 (2)
0.496 ∙ 6 = 2.976 (2)
0.976 ∙ 6 = 5.856 (5)
0.856 ∙ 6 = 5.136 (5)
0.136 ∙ 6 = 0.816 (0)
0.816 ∙ 6 = 4.896 (4)
0.896 ∙ 6 = 5.376 (5)
0.376 ∙ 6 = 2.256 (2)

0.201₁₀=0.11122550452₆

Теперь осталось соединить результаты перевода. Таким образом: 358.201₁₀=1354.11122550452₆

Таблица соответствия популярных систем счисления

Десятичная система	Двоичная система	Восьмеричная система	Шестнадцатеричная система
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

• Какое число еще хотите перевести?

  * Все поля обязательны
• Введите число: Дробное число вводите через точку
• Основание системы счисления: Введите от 2 до 16
• В какую систему перевести: Введите от 2 до 16
• Перевести